Thinking about bridge tilt angles and apparent top thickness’
When an instrument such as a guitar is strung up, the string tension affects the neck and top. The neck has a tendency to come up a little. And the top tends to go down in front of the bridge and up in back of the bridge.
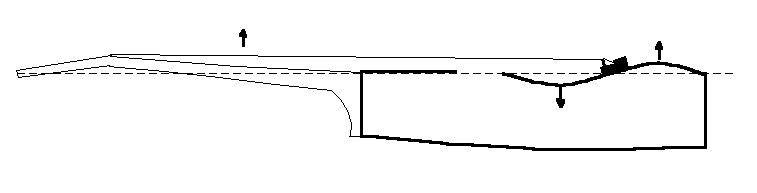
In one of his publications (see LINKS below) , Trevor Gore suggested that when a guitar is strung up, the bridge should tilt no more than 2 degrees. I thought it might be interesting to see whether I could use existing engineering formulas to see if it was possible to guess the thickness of a top that would only allow a 2 degree rotation. Also it would be interesting to see if there was a link between (1) the properties associated with this amount of rotation and (2) the top compliance measurements that I espouse in my book “Left-brain Lutherie” (shameless promotion of book).
In order to find formulas for such a calculation, I used “Roarke’s Formulas for Stress and Strain” (see LINKS below), a really interesting source of material with many possible applications to lutherie. The link leads to a free PDF for the book.
Today I’d like to point the reader to Roarke’s page 494, Case 21b, trunnion loading on an annular plate with a fixed outer edge shown in the figure below. In this case, I’m suggesting that this situation may be similar to the lower bout of a guitar with the top “fixed” to the sides of the guitar and the bridge acting as the trunnion. The strings pulling on the bridge will cause the bridge to rotate as mentioned above.
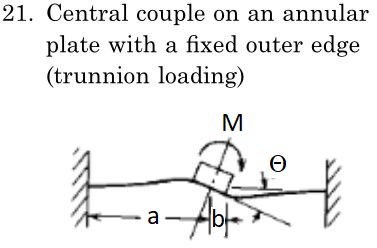
So let’s begin with the formula for case 21b and explanations for each term.
(1) Θ = (α*M) / (E*t^3)
Θ = the angle of rotation in radians; to get radians from degrees, multiply degrees * (π/180)
α = the ratio (a/b) of the width of the trunnion (bridge) to the width of the plate
M = torque on the trunion; in this case string pull x saddle height, inlbs
E = Young’s modulus of the plate, psia; we’ll use Eave as described in “Left-Brain Lutherie”
t = thickness of the plate, in.; we’ll use using apparent thickness which includes the original plate thickness plus the stiffness added by the braces.
My objective here is to see what sort of apparent plate thickness will be needed to be stiff enough so that the bridge won’t torque more than the 2 degree value. So we need to re-arrange equation (1) and solve for t, the apparent plate thickness.
(2) t = \sqrt[3]{(α*M)/(E*Θ)}
OK, so let’s put in some numbers for the above.
Θ = 2 degrees * (π/180) = 2 * (0.0175) = 0.035 radians
For M I’m using a saddle height of 3/8” and a string pull of 86 lbs to represent a guitar with low tension strings. M = 0.375 * 86 = 32.3 inlbs
For Eave I’m using a plate value of 560,000 psia. This is for a moderately stiff plate.
For α I’m using an a/b ratio of 0.1. From the Case 21b table the value is 1.15
Plugging these values into equation (2) and solving for t, we get a value of o.127 in or 127 mil for the apparent plate thickness. Apparent thickness includes the bracing underneath the top. It is also important to note at this point that the 127 mil value is just one case. Anyone having my book can go to tables 11 and 12 in Chapter 5 and play with other numbers to get a better sense of the range of values with different saddle heights, string tensions, values of Eave , etc.
Now let’s take a look at my predictive compliance spreadsheet ( EstimatedComplDeflect.xls ) that comes with the book. My objective with this spreadsheet was to create a predictive model of top compliances for different sized guitar family instruments. Starting values for variables are input by the maker: Eave , saddle height, lower bout radius, plate thickness and string tension. Calculated values include apparent plate thickness, string torque, top deflection from string torque and suggested compliance range around the bridge area. In this case, I’m going to use the values for the guitar example.
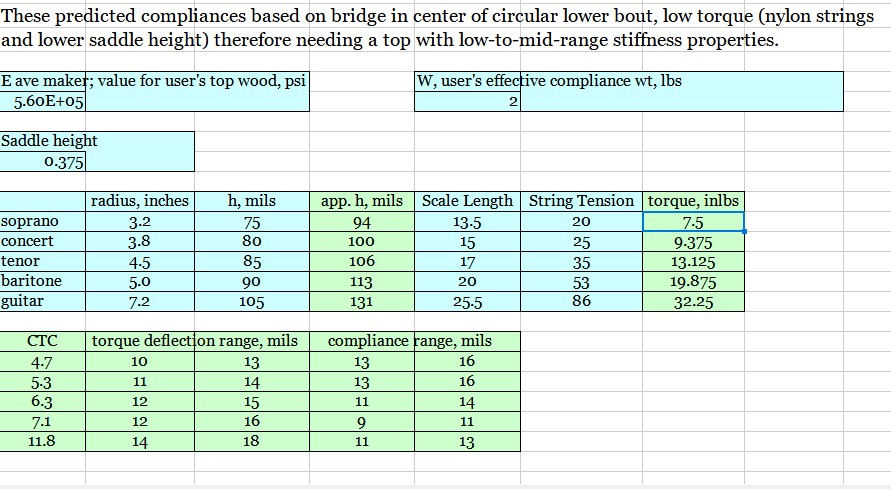
It is remarkable to me, although perhaps fortuitous, how close the calculated value of 127 mils from equations (1) and (2) is to the predictive spreadsheet value of 131 mils above given that the two approaches are independent of one another. Yes, some of the same variable values were used in both cases but the formulas are totally different.
In any case, it would be great if readers play with the “trunnion” and compliance formulas to have a sense of whether my above calculations are useful in helping with instrument longevity and optimization for the instruments they build.
LINKS:
Trevor Gore article:
https://pubs.aip.org/asa/poma/article/12/1/035001/994561/Wood-for-Guitars
Roarke’s Formulas for Stress and Strain:
https://archive.org/details/RoarksFormulasForStressAndStrain7thEd