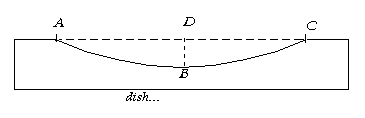Calculating the Radii of Ukulele and Guitar Arches
If you enjoy the technical side of things, please consider buying my book “Left-brain Lutherie” . Although no longer sold by StewMac, you can buy directly from me.
It’s fairly routine to read about an arch of so many feet radius for the top of a guitar and another for a different number of feet radius for the back of the guitar, but how do you go about measuring these radii? That is, if you wanted to make a form for a router to make a dish two feet wide with a radius of 10 or 15 feet how do you go about estimating the shape of the curve?
Where to look? Probably any beginning geometry text would have sufficient information, but I found a proper figure on page 398 of the CRC Standard Mathematical Tables, Chemical Rubber Publishing Company, Cleveland, OH 1959.
I don’t claim that the following analysis is the most elegant, but it works. I’d be happy to hear from others regarding such calculations and be willing to offer their analyses as well. Figure 1 shows the arch cross-section.
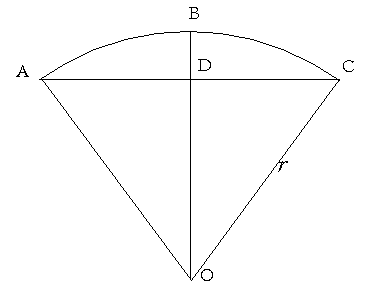
Arch Cross-Section
Figure 1. Plan View of Arch components
The arch under consideration has a number of components : 1) the arc of the arch shown as the solid line ABC; 2) the linear width of the arch, solid line ADC (also termed a chord); 3) the radius of the arch, solid lines AO, BDO and r; the height of the arch, BD. Note that angles BDC and ODC are right angles and that OBCO is an equilateral triangle.
For our first case, let’s try to find out the radius of the back of a classical guitar. The width of the lower bout (ADC) is 14″ and by placing a straightedge gently on the top of the arched back we can measure a distance of 1/4″ between the edges of the back and the edge of the ruler (BD). So we know the value of BD (1/4″) and CD (7″) and want to know r.
Guitar Cross-Section
Figure 2. Guitar Side View
So,
BD = r – OD
or,
r = BD + OD
and with the help of Pythagoras
OD2 = r2 – CD2
so,
r = BD + (r2 – CD2) 1/2
rearranging and solving for r,
r = (BD2 + CD2)/(2 x BD)
Thus for our example,
r = (.252 + 72)/(2 x .25)
= 98″ = 8.17′
Now let’s try a different case. Suppose that we want to create an arc that will guide a router to cut a dish shape into a form for arching the top of a guitar to a radius of 20′. If the dish will be say, 18″ wide then we need an arc probably 24″ wide. So if ADC is 24″ then CD is 12″. r is 20′ which is equal to 240″. At this point, we need to solve for BD using CD and r.
Guitar Cross-Section
Figure 3. Dish Side View
From above,
BD = r – OD
and
OD2 = r2 – CD2
so,
BD = r – (r2 – CD2)1/2
Therefore for this second example,
BD = 240″ – (2402 – 122)1/2
= 0.30″
The name of the spreadsheet for the two problems described above is ArcCalcs.xls and is an Excel spreadsheet.
ArcCalcs (to download double-click or option-click)
I enjoy writing these pages and hope that they are interesting and useful to the reader. I’ve stopped building at this time and still need to generate some income in order to continue to expand this website with more useful articles. If this page was helpful to you and you would like to make a $5.00 donation in order to have more pages like it, please use the donation button below. Thank you.